lecture 20. Cramer's Rule, Inverse Matrix, and Volume

https://www.youtube.com/watch?v=QNpj-gOXW9M&list=PLE7DDD91010BC51F8&index=21 

이번 강의는 determinant의 응용에 대한 강의이다.

 

1. inverse matrix

A의 inverse matrix는 \(\frac{1}{det(A)}\)와 cofactor matrix의 transpose의 곱이다. 2X2 matrix로 예를 들어보면 cofactor matrix는 A transpose에서 (1,2), (2,1)의 부호만 바꾼 형태가 된다.

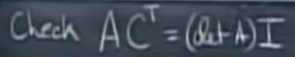
이 식이 성립하는지 확인하여 정말 \(A^{-1}=\frac{1}{det(A)}C^T\)인지 확인할 수 있다. 저번 시간에 배운 내용을 활용하면 대각선 부분이 det(A)가 되는 것은 확인할 수 있다. 

이제 남은 것은 대각선을 제외한 부분이 0가 되는지 확인하는 것이다. 만약 2개의 동일한 row가 있으면 determinant가 0이 된다. 대각선을 제외한 부분은 동일한 1번째 row와 마지막 row가 동일한 matrix의 determinant과 같으므로 0이 된다.

2. cramer's rule

determinant를 사용해 Ax=b의 solution을 구할 수 있다.

$$x=A^{-1}b=\frac{1}{det(A)}C^Tb$$

이렇게 A inverse의 식을 활용해 solution을 구할 수 있다. cramer's rule은 위의 식에서 \(frac{1}{det(A)}C^Tb\)에 대한 법칙이다.

이런 식으로 \(frac{1}{det(A)}C^Tb\)의 성분을 찾아내는 것을 cramer's rule이라고 하면 여기서 \(B_j\)는 j번째 column이 b로 교체된 것이다. 이것을 활용하면 x를 구할 수 있다. 하지만 cramer's rule에는 determinant 계산을 너무 많이 해야 한다는 문제가 있기 때문에 실제로 Ax=b를 계산할 때 사용하는 것은 추천하지 않는다.

 

3. det A = volume of box

determinant의 값이 음수가 될 수도 있기 때문에 det A의 절댓값이 volume of box와 같다는 것이 정확한 표현이다.

만약 A가 identity matrix라면, 마치 unit cube와 같이 생각할 수 있고 volume은 1이 된다. 그리고 edge의 위치를 바꿔도 box의 형태는 바뀌어도 volume 자체는 바뀌지 않는다. 여기서 determinant property 1, 2번이 성립한다. \(Q^TQ=I\)이므로 property 9, 10에 의해 Q의 determinant는 1 또는 -1임을 알 수 있다. 1개의 edge가 2배가 되면 volume도 2배가 되므로 property 3(a)도 성립한다. property 3(b)에 대한 설명은 책에 있다.

위의 내용을 통해 det A = volume of box이며 determinant의 공식이 box의 volume을 구하는 상황에도 적용된다는 것을 보았다. 예시를 보자.

사각형의 높이와 밑면의 길이로 구하려면 계산이 복잡하지만 determinant를 사용해 간단하게 계산하였다. 만약 삼각형을 구하고 싶으면 위의 식에 1/2만 곱하면 된다.

원점에서 시작하지 않는 경우라면 어떻게 할까? 이런 경우 위와 같이 풀면 된다. row2에서 row1을 빼고 row3에서 row1을 빼면 마치 (\(x_1,y_1\))을 (0,0)으로 한 것과 같다.