lecture 18. Properties of Determinants

https://www.youtube.com/watch?v=srxexLishgY&list=PLE7DDD91010BC51F8&index=19 

 

이번 강의에서는 determinant의 property 10개를 배운다.

determinant는 square matrix에서 적용되는 숫자이다. A의 determinant는 det(A) 또는 \(\left | A \right |\)라고 쓴다.

그리고 determinant를 계산할 때는 bracket 대신 vertical bar를 쓴다. \(\begin{bmatrix}
1 & 1\\ 
1 & 1
\end{bmatrix}\) 이렇게 쓰는 대신 \(\begin{vmatrix}
1 & 1\\ 
1 & 1
\end{vmatrix}\)이렇게 써야 한다. 아래는 determinant의 10가지 property이다.

 

1. identity matrix의 determinant는 1이다. (\(det(I)=1\))

 

2. row exchange는 determinant의 부호를 바꾼다.

여기서 permutatoin matrix를 예로 들수 있다.permuation matrix는 identity matrix의 row exchange로 나온 것으로 볼 수 있으며 permutation matrix의 determinant는 1 또는 -1이다. row를 짝수번 바꾸면 1이고 홀수번 바꾸면 -1이다.

 

3a. matrix의 특정 row에 t를 곱하면 determinant는 t배가 된다.

3b. 특정 row에 값을 더하면 아래의 그림과 같이 쓸 수 있다. (이것은 det(A+B)=det(A)+det(B)를 의미하지 않는다.)

4. 2개의 동일한 row가 있으면 determinant는 0이 된다.

동일한 row끼리 row exchange를 해보자. 동일한 row끼리 교체하였기 때문에 matrix에는 어떠한 변화도 없을 것이고 determinant도 바뀌지 않는다. 2번 property에 의해 row exchange를 하면 determinantd의 부호가 바뀌어야 하는데 이 경우 determinant가 바뀌지 않는다. 여기서 determinant가 0가 된다는 것을 알 수 있다.

 

5. row i에 l를 곱한 후 row k에서 빼도 determinant는 변하지 않는다.

이 property는 elimination을 하며 row끼리 연산을 해도 determinant는 변하지 않는다는 것을 의미한다. 따라서 elimination을 통해 A를 U로 만들어도 determination은 변하지 않는다. 증명 과정은 아래와 같다.

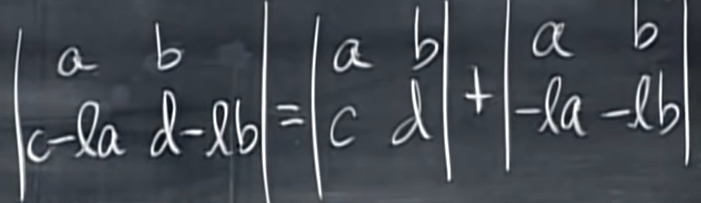
여기서 property 3에 의해 \(\begin{vmatrix}
a & b\\ 
-la & -lb
\end{vmatrix}\)은 \(-l\begin{vmatrix}
a & b\\ 
a & b
\end{vmatrix}\)로 쓸 수 있다. 그런데 이것은 동일한 row가 2개 있으므로 0이 된다. 그래서 \(\begin{vmatrix}
a & b\\ 
c-la & d-lb
\end{vmatrix}=\begin{vmatrix}
a & b\\ 
c & d
\end{vmatrix}\)이다.

 

6. row of zeros는 determinant of A를 0으로 한다.

elimination 후 0인 matrix는 inverse matrix가 존재하지 않는 singular matrix이고 이것의 determinant는 0이 된다. 6번 property가 성립하는 이유는 property 3a를 사용하여 이해할 수 있다. row of zeros는 property 3a에서 t=0인 경우로 생각할 수 있기 때문이다.

 

7. upper triangular matrix의 determinant는 이것의 diagonal component의 곱과 같다.

upper triangular matrix는 elimination을 통해 diagonal component만을 제외하고 모두 0으로 만들 수 있다. 그리고 이런 matrix는

이러한 형태로 쓸 수 있다. 그래서 upper triangular matrix의 determinant는 이것의 diagonal component의 곱이 되는 것이다. 이것은 pivot들의 곱이라고도 할 수 있다.

 

8. det(A)는 A가 singular이면 0이다. 만약 0이 아니면 A는 invertible 하다.

det(A)가 0이면 row of zeros가 있는 것이고 이것은 A가 singular라는 뜻이다. det(A)가 0이 아니라는 것은 inverse matrix가 있다는 말이다. 그럼 elimination을 통해 A를 U로 만들고 property 7을 사용해 determinant를 구할 수 있다.

 

9. det(AB) = (det A)(det B)

\(AA^{-1}=I\)이므로 \(det(A^{-1})=\frac{1}{det(A)}\)이다.

det 2A는 무엇일까? det(A)+det(A)라고 할 수도 있겠지만 이는 틀린 표현이다. property 3a에 의해 \(det(2A)=2^ndet(A)\)이다. det(AB) = (det A)(det B)은 성립해도 det(A+B) = (det A)+(det B)는 성립하지 않는다.

 

10. \(det(A^T)=det(A)\)

row exchange는 부호를 바꿨듯이 column exchange도 부호를 바꾼다.

위의 사진은 property 10의 증명 과정이다. \(L\)의 대각선에는 1이 있고 이는 \(L^T\)도 마찬가지이다. 그래서 \(L\), \(L^T\)의 determinant는 0이다. \(U\)와 \(U^T\)의 determinant는 대각선에 있는 숫자들의 곱이다. 대각선에 있는 숫자들은 transpose를 해도 바뀌자 않으므로 \(U\)와 \(U^T\)의 determinant는 동일하다. 이렇게 증명할 수 있는 것이다.