lecture 22. Diagonalization and Powers of A

https://www.youtube.com/watch?v=13r9QY6cmjc&list=PLE7DDD91010BC51F8&index=23 

 

1. diagonalization

eigenvalue와 eigenvector를 사용하여 diagonalization을 할 수 있다. S를 eigenvector로 이루어진 matrix라고 하자. S를 만들기 위해 n개의 independent eigenvector가 사용된다.

\(Ax=\lambda x\)이므로 위와 같이 쓸 수 있고

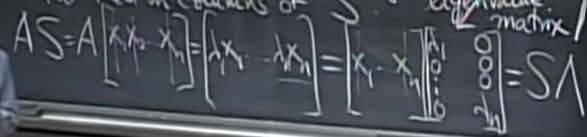
식을 정리하면 이렇게 쓸 수 있다. \(AS=S\Lambda\)이며 \(\Lambda\)는 eigenvalue가 대각선에 위치하는 matrix가 된다. \(AS=S\Lambda\)이므로

$$S^{-1}AS=\Lambda$$

$$A=S\Lambda S^{-1}$$

이것은 LU나 QR을 사용했던 것과는 다른 새로운 factorization이다. 만약 \(A\)가 아니라 \(A^2\)이면 어떻게 될까? 우선 \(Ax=\lambda x\)에서 시작하자.

이런 방식을 \(A=S\Lambda S^{-1}\)에도 적용할 수 있다.

그리고 동일한 방식으로 이런 공식을 얻을 수 있다.

eigenvalue와 eigenvector는 powers of a matrix의 이해를 돕는다. matrix의 k제곱이 0으로 하는 것을 stable matrix라고 생각한다. stable matrix가 되는 조건이 무엇일까? \(S\), \(S^{-1}\)의 값은 변하지 않으므로 \(Lambda\)의 값이 0이 되야 한다. 이것이 되기 위해서 eigenvalue가 모두 1보다 작아야 한다.

그런데 앞에서 언급한 내용이 성립하기 위해서는 n개의 independent eigenvector가 있어야 한다. 그리고 이 내용은 이렇게 정리할 수 있다.

2. repeated eigenvalue

10 by 10 identity matrix를 생각해보자. 10개의 동일한 eigenvalue를 구할 수 있다. 하지만 identity matrix의 모든 column이 eigenvector이므로 10개의 identity eigenvector를 구할 수 있다. 이 경우에는 repeated eigenvalue가 문제가 되지 않는다. 오히려 이미 diagonalization된 matrix라고 생각할 수 있다. 하지만 triangular matrix에서는 달라진다. 이전 강의에서 설명한대로 이 형태에서는 eigenvector를 충분히 얻을 수 없다.

예제를 보자. \(A=\begin{bmatrix}
2 & 1\\ 
0 & 2
\end{bmatrix}\)라는 matrix가 있을 때 eigenvalue는 2, 2이다. 그리고 eigenvector는 \(x=\begin{bmatrix}
1 \\ 
0 
\end{bmatrix}\)이다. 여기서 eigenvalue는 2번 반복되기 때문에 algebraic multiplicity는 2가 된다. 그리고 \(x=\begin{bmatrix}
1 \\ 
0 
\end{bmatrix}\)는 (A-2I)의 nullspace가 되므로 nullspace의 dimension은 1이 되고 따라서 geometric multiplicity는 1이다.

 

3. difference equations

주어진 방정식을 풀어보자. \(u_0\)로 시작하고 모든 단계마다 A를 곱하는 방정식이 있다. k단계 후에서는 \(u_k=A^ku_0\)이다.

이제 difference equation을 풀어보자. 예를 들어 \(u_{100}\)을 구해본다고 하자. \(u_k=A^ku_0\)를 사용하여 \(u_{100}\)를 구할 수 있다. 이때 \(A^kx=\lambda^k x\)를 사용해 \(A^{100}\)를 구할 수 있으며 그 결과 식은 아래와 같이 구할 수 있다.

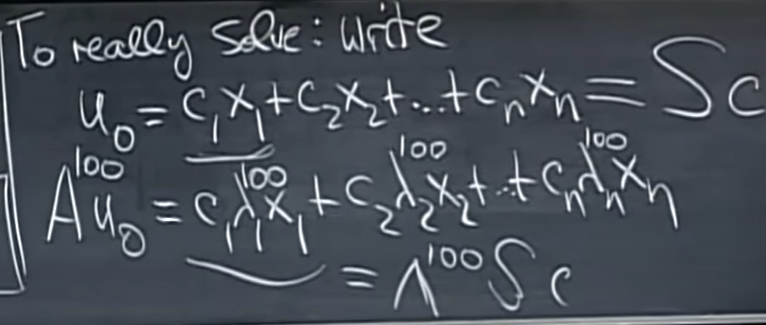
4. Fibonacci example

difference equation에서 배운 내용으로 fibonacci 문제를 풀어보자. fibonacci 수열의 100번째 숫자인 \(F_100\)을 어떻게 구할까?

Fibonacci rule을 적어보자.

이것은 second order differential equation이다. 앞에서 한 것은 first derivatives에 적용되기 때문에 first derivatives를 얻어야 한다. 여기서 trick을 사용한다. \(u_k=\begin{bmatrix}
F_{k+1} \\ 
F_k
\end{bmatrix}\)으로 하자. 그리고 equation \(F_{k+1}=F_{k+1}\)을 추가하자. 그러면 

이렇게 쓸 수 있다. \(A=\begin{bmatrix}
1 &1 \\ 
1 &0
\end{bmatrix}\)의 eigenvalue를 구하면

fibonacci number를 control하는 것은 eigenvalue이고 fibonacci number는 계속 증가한다. 따라서 \(\lambda_1=1.618...\)을 사용해 \(F_100\)에 대한 정보를 얻을 수 있다. 앞에서 설명했던 내용을 사용해보자.

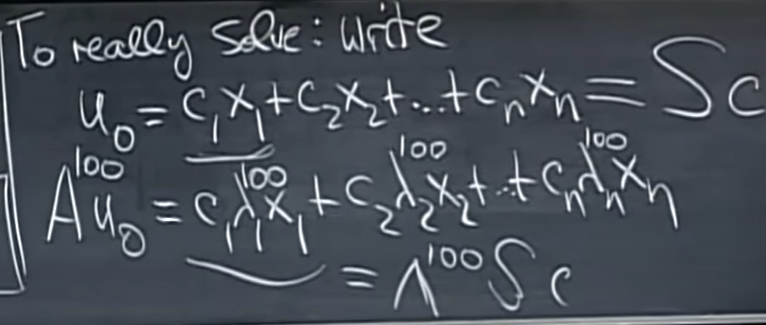
여기서 A는 2 by 2 matrix이므로 \(\lambda_1\), \(\lambda_2\)까지만 보면 되고 \(\lambda_2\)는 절댓값이 1보다 작으므로 100제곱 하면 0에 가까운 값을 가질 것이다. 따라서 \(u_{100}\)은 \(c_1x_1\)에 \(\lambda_1\)을 100번 곱한 값이 될 것이다. 마지막으로 \(u_0\)와 eigenvector를 구해보자. \(u_0\)는 \(\begin{bmatrix}
F_{1} \\ 
F_0
\end{bmatrix}\)이므로 \(u_0=\begin{bmatrix}
1 \\ 
0
\end{bmatrix}\)이다. 그리고 eigenvector는 

이제 x와 \(u_0\)를 알았으니 \(c_1\), \(c_2\)를 구할 수 있다.