lecture 16. Projection Matrices and Least Squares

https://www.youtube.com/watch?v=osh80YCg_GM&list=PLE7DDD91010BC51F8&index=17 

projection matrix

projection에 대한 두가지 성질이 있다.

1. If b in column space \(Pb=b\)

2. If b is perpendicular to column space \(Pb=0\)

 

첫번째 성질부터 확인해 보자.

\(Pb=A(A^TA)^{-1}A^Tb\) 이며 b가 column space에 있으므로 b대신 Ax를 사용하여 \(Pb=A(A^TA)^{-1}A^TAx\)로 적을 수 있다. 여기서 \(A^TA\)는 \((A^TA)^{-1}\)에 의해 \(I\)가 된다. 그래서 \(Pb=Ax\)가 되므로 \(Pb=b\)이다.

두번째 성질도 확인해 보자.

\(Pb=A(A^TA)^{-1}A^Tb\)에서 b가 column space에 perpendicular하므로 \(A^T\)의 nullspace에 있으며 \(A^Tb=0\)이다. 그래서 \(Pb=A(A^TA)^{-1}A^Tb=0\)인 것이다.

 

column space와 \(A^T\)의 null space가 있고 vector b가 있다. b를 column space에 projection한 것이 p이고 \(A^T\)의 null space에 projection한 것이 e가 된다. 그리고 b=p+e이다. b는 p와 e의 합으로 이루어 지므로 b에서 p를 뺀것은 e가 된다. p=Pb이므로 e=(I-P)b로 쓸 수 있다. \(P\)는 symmetric하고 \(P^2=P\)이므로 \(I-P\)는 symmetric하고 \((I-P)^2=(I-P)\)이다.

 

line fitting

저번 시간에 소개했던 내용을 다시 다뤄보자.

(1,1), (2,2), (3,2)을 통과하는 직선을 찾고자하지만 이런 3점을 모두 통과하는 직선은 존재하지 않으므로 overall error가 가장 작은 best line을 찾을 것이다. 찾고자 하는 직선을 y=C+Dt로 하면 위의 사진에서 볼 수 있듯이 3개의 식을 얻을 수 있으며 이 식은 Ax=b 형태로 나타낼 수 있다.

b=\([1 2 2]^T\)이다. 교수님이 잘못 적으셨다.

b는 A의 column space에 존재하지 않으므로 해가 존재하지 않는다. 그래서 가장 error가 작은 solution을 구하기로 하며 이것을 least sqaures solution이라고 한다.

least square solutioin

Ax와 b 사이의 거리가 error 이다. error를 줄이기 위해 error vector의 length를 작게 만들어야 하고 음수가 나오지 않게 하기 위해 제곱을 한다. 첫번째 점에 대한 error는 \(e_1\), 두번째 점에 대한 error는 \(e_2\), 세번째 점에 대한 error는 \(e_3\)로 하자. line 위에 \(p_1\)이 있을 때, line과 \(p_1\) 사이의 거리가 \(e_1\)이 된다. 나머지 \(e_2\), \(e_3\)도 똑같이 생각하면 된다. 여기서 overall error는 \((e_1)^2+(e_2)^2+(e_3)^2\)이다.

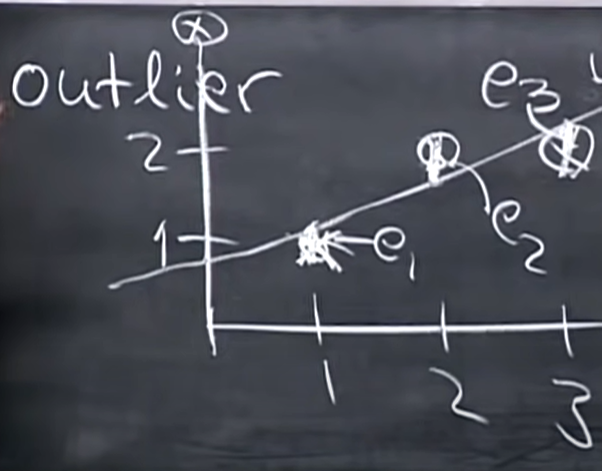
만약 이렇게 4번째 점을 갖게 된다면 error가 매우 커질 것이다. 이런 것을 outlier라고 한다.

 

line을 구하기 전에 이 문제를 vector space의 관점에서 잠깐 보자.

b는 \(\begin{bmatrix}
1\\ 
2\\ 
2
\end{bmatrix}\)가 되고 A의 column들은 column space의 basis가 된다. 그리고 column space 위의 점 p는 \begin{bmatrix}
p_1\\ 
p_2\\ 
p_3
\end{bmatrix}이다.

 

다시 line 구하기로 돌아오자. Ax=b의 solution을 찾을 수 없으니 이전 강의들에서 배운 방식대로 best solution을 찾을 것이다.

$$A^TA\hat{x}=A^Tb$$

이 식의 solution이 best solution이 되고 best solution을 사용해 best line을 찾을 수 있다.

위의 사진을 보자. augmented matrix가 있다. 이것의 왼쪽 성분은 \(A^TA\), 오른쪽 성분은 \(A^Tb\)이다. augmented matrix 옆에 있는 식은 matrix를 방정식으로 만든 것이다. 이 방정식은 normal equation이라고 한다. 이 방정식을 풀면 \(C=\frac{2}{3}\), \(D = \frac{1}{2}\)이다. 결국 우리는 2/3+1/2t라는 best line을 구한 것이다.

 

참고로 normal equations는 Calculus로도 찾을 수 있다.

error는 이런식으로 표현할 수도 있다. 이 식을 C에 대해 편미분 하고, D에 대해 편미분 한다면 2개의 식을 얻을 수 있는데 이렇게 하면 matrix를 사용해 구한 normal equation와 동일한 식을 구할 수 있다.

 

line을 구했으니 직접 숫자를 대입해 \(p_1\), \(p_2\), \(p_3\)의 크기를 구할 수 있다. 이것들은 각각 7/6, 10/6, 13/6이다. 그리고 p-b로 error를 구할 수도 있다. \(e_1\), \(e_2\), \(e_3\)의 크기는 각각 1/6, -2/6, 1/6이다.

vector space를 설명하는 그림에서 보았듯이 p와 e는 서로 perpendicular하다. 그래서 p, e를 내적한 결과는 0이 된다.

 

\(A^TA\)의 inverse matrix

\(A^TA\)가 inverse matrix를 갖기 위해서는 다음과 같은 조건이 있다.

"If A has independent columns then \(A^TA\) is invertible"

이것을 증명해 보자.

만약 \(A^TAx=0\)이라고 가정하면 x=0이여야 위의 조건이 성립한다. 우리는 nullspace에 0만 존재한다는 것을 보여야 한다. 양변에 \(x^T\)를 곱하자.

\(x^TA^TAx=0\)이고 이것은 \((Ax)^TAx=0\)이다. 이것이 만족하기 위해서는 Ax=0이여만 한다. 이때 A가 independent columns를 갖고 있으므로 x는 0이여야 한다.

 

이제 column이 반드시 independent인 경우를 보자

columns definitely independent if they are perpendicular unit vectors.

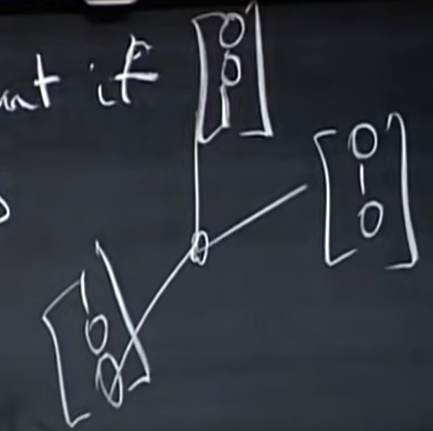
이렇게 3개의 unit vector가 예시가 될 것이다. perpendicular unit vectors는 perpendicular하기 때문에 ortho-, unit vector이기 때무에 -normal을 붙여 orthonomal vector라고 한다. orthonomal vector의 예로 

이런것도 있다. 다음 시간에는 orthonomal vector가 왜 중요한지, basis를 선택해 orthonomal vector를 만드는 법을 배울 것이다.